Climate Explorer — Help
Empirical Event Attribution
Sometimes there is enough historical data to detect a trend in the observational record. In this case one can attempt a two-step attribution process:
  1. Compute the observed trend in the phenomenon under consideration (excluding the event itself).
  2. Relate the event quantitatively by physical and observational arguments to a quantity for which a model-based attribution study has been performed
Note that these routines are being developed and are not yet as stable as other parts of the Climate Explorer. Please report bugs and oddities. I give two examples, on the seasonal and daily time scales.
Example 1: Russian heat wave 2010
The summer of 2010 was very hot in large areas of European Russia. The following analysis has been published in Otto et al, GRL, 2012, albeit with a data up to 2011 only.

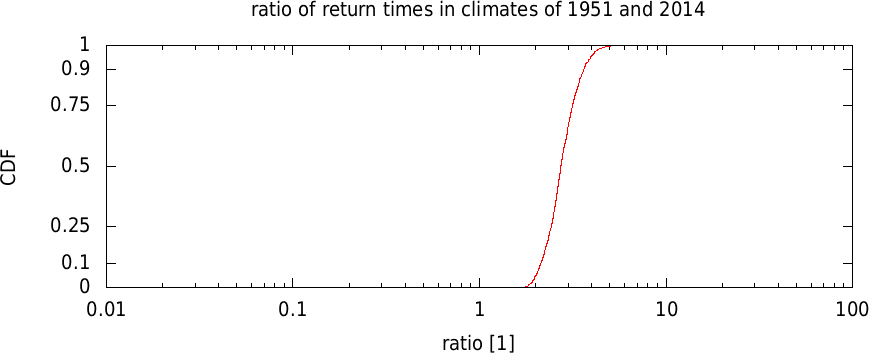
The area average 50°-60°N, 35°-55°E in the GISTEMP 1200 dataset for July is shown below.

July temperature in the area of the heat wave, 50°-60°N, 35°-55°E in the GISTEMP 1200 dataset.
temperature in the heat wave area in July, GISTEMP 1200

This immediately presents a problem. The low-pass filtered temperature follows the global mean temperature well after 1950, but has very high values also in the 1930s. The decision whether to include these (Dole et al, GRL, 2011) or not (Otto et al, 2012) is a subjective one. On the basis of observed discontinuities in individual station series during the second world war we concluded that the cooling from the 1930s to the 1950s is likely an artefact caused by station changes and we started our analysis in 1950.

This series has to be analysed with a GPD fit, where we shift the distribution with the global mean temperature. There is evidence that high extremes increase faster than the mean, but we do not have enough information to take that into account in this fit. It should be investigated how this affects the result. We take a threshold of 80% and constrain the shape parameter ξ to be roughly in the interval ±0.2 to get better convergence (especially in the bootstrapped error margins). The fit gives a small ξ and the fitted line agrees well with the data points, so this is a reasonable choice. The fit results are

Jul GISS_1200_T2m/SST_anom_35-55E_50-60N tempanomaly [Celsius] dependent on GISS global temperature
 covariatie 1950 = -0.11521
 covariatie 2010 = 0.57083
parameteryearvalue95% CI
N:  63 
Fitted to GPD distribution H(x+a') = 1 - (1+ξ*x/b')^(-1/ξ)
with a'= a+αT and b' = b
a: 1.337 1.138... 3.529
b: 0.732 0.192... 0.872
ξ: -0.032 -0.049... 0.115
α: 1.906 -0.518... 10.719
return period 2010 1950 2635.9 13.636 ... 0.31326E+09
(value 4.8858 ) 2010 318.17 2.1290 ... 24597.
 ratio 8.2847 0.22238 ... 0.43287E+07
The central value of the trend is almost two times faster than the global mean temperature rise, but with a large uncertainty that includes zero. The return time of this event still is 300 years (with a 95% CI starting at 2 years) in the current climate, but this number is artificially enhanced by choosing an area that describes the worst part of the heat wave. This area covers roughly 1% of the land surface of the earth, so we would expect a heatwave anywhere on land with a return time of 300 years once every three years on average.
Jul index GISS 1200 T2m/SST anom 35-55E 50-60N beginning 1950 with the effects of GISS global temperature linearly subtracted from the position parameter a, referenced at 1950 and 2010
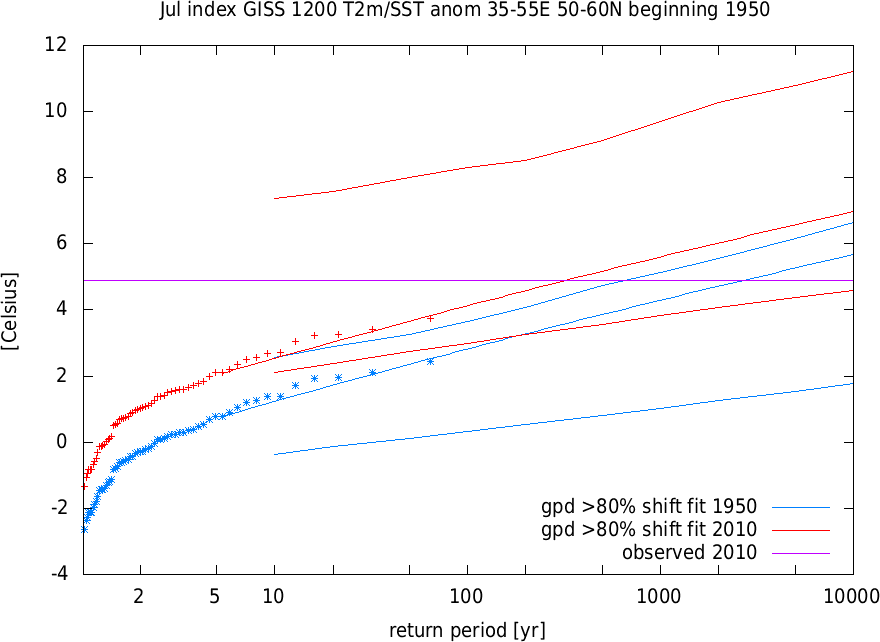
Estimate of return period of temperature extremes, corrected for global temperature increase

Based on the trend over 1950-2014, heat waves like his have become more likely with a p-value p<0.1: the CDF crosses 1 at around 0.07:

CDF of the ratio of the return times of 2010 Jul index GISS 1200 T2m/SST anom 35-55E 50-60N beginning 1950 in the climates of 2010 and of 1950
CDF of the difference in return times of 2010 and 1950
Repeating the exercise with all data, rather than just after 1950, gives much smaller statistical uncertainties, with a significant trend and an increase in frequency of a factor 1.8 to 300 (p<0.02). This shows that the actual numbers depend strongly on the choices made in the analysis, this should be taken into account in the analysis. The second step is that the July temperature in Russia is strongly related to larger scale temperatures, the rise of which has been attributed to anthropogenic factors. This can also be seen by the CMIP5 climate model results for this area from the KNMI Climate Change Atlas. In fact there is good quantitative agreement, with the climate model rise also about 1.5 °C.
Temperature change 50-60N, 35-55E Jul-Jul wrt 1951-1980 AR5 CMIP5 subset. On the left, for each scenario one line per model is shown plus the multi-model mean, on the right percentiles of the whole dataset: the box extends from 25% to 75%, the whiskers from 5% to 95% and the horizontal line denotes the median (50%).
CMIP5 temperature change in 50-60N, 35-55E, in July
'
Example 2: Long Island precipitation 2014
On 13 August 2014 Islip, New York, received more than 300 mm of rain in 24 hours (most of it in a few hours). First we compute the return times of such an event and whether this has changed over time. The station is included in the GHCN-D database, just search for "Islip". There are two stations, the airport has the longest time series (31 years) and the highest value (343.2 mm). However, a single time series is not enough to compute return times. As the decorrelation scale of the most intense precipitation is relatively small, we collect 50 time series around the coordinates of the Islip airport station, 40.79°N, -73.10°E. The two Islip stations (separated by about 12 km) have similar values for 13 august 2014, but other stations in the area have much lower values, as can quickly be checked by plotting the observed value stations. This shows that we must demand a station distance of a bit more than 12 km, say 0.2°, to be able to consider them independent. The resulting dataset covers Long Island and some adjacent inland areas, see the map below.

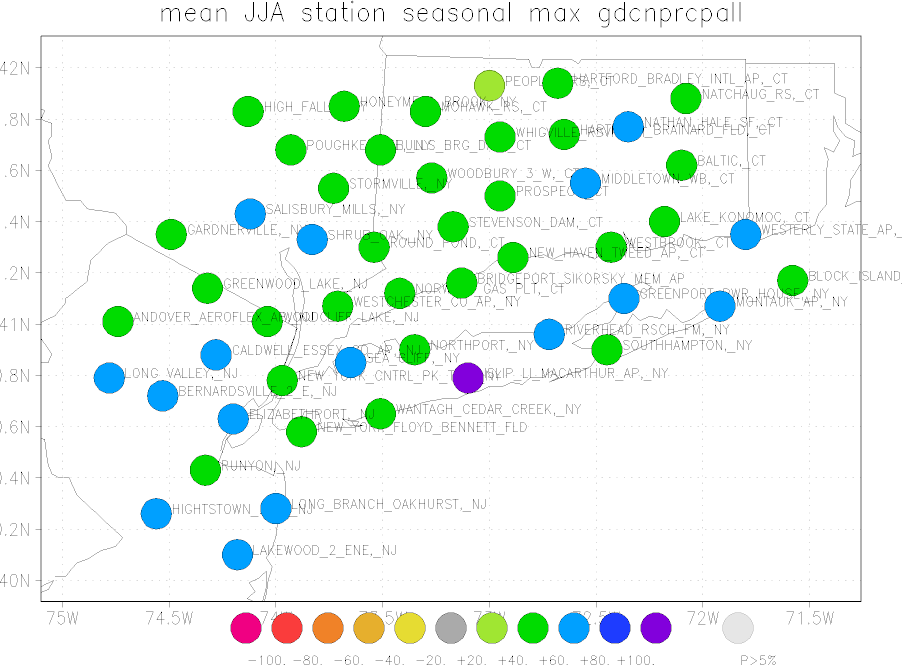
Next we have to check whether these stations are comparable in their rainfall climate. As a first check I computed the mean of the maximum precipitation in June-August. The first time this takes a while as the station data has to be converted from the GHCN-D format into the Climate Explorer format. Subsequent operations on the same data are much faster. There are no obvious structures in the map, such as more intense showers on the coast, to the south or over the city of New York. We therefore consider all these stations identically distributed.

Mean of the highest daily precipitation in June-August at 50 stations around Islip, NY separated by at least 0.2°
mean max daily summer precipitation

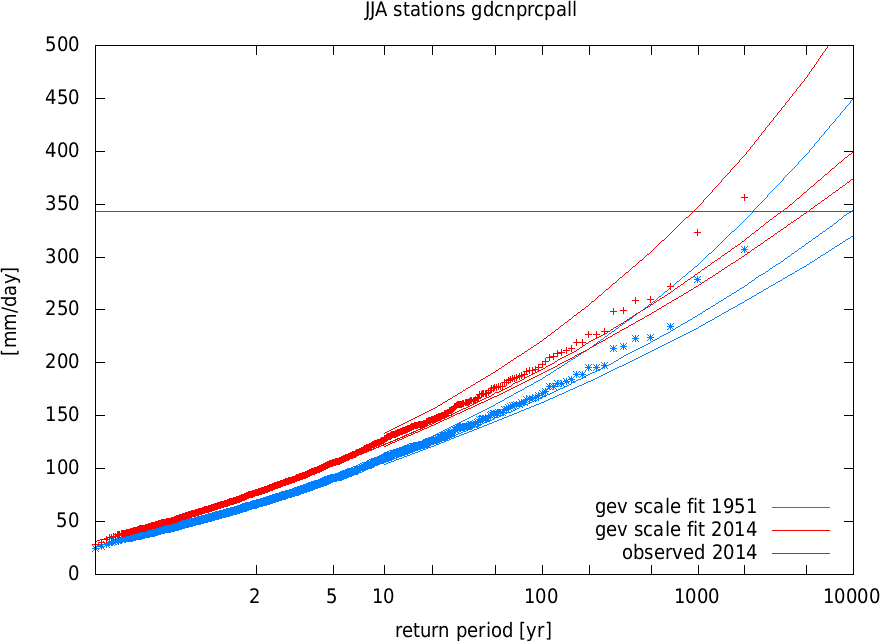
Next we can compute extreme value statistics. For this we take summer maximum of precipitation and fit it to a GEV distribution. (NOTE: The GPD(T) routine still has issues at this moment, 4 September 2014.) We consider June-August again to exclude tropical storms and winter storms. The summer maximum can be specified in two ways: either by operating on the time series after selecting the set, or in the form 'trends in return times of extremes'. The latter offers more flexibility, but gives slightly different results at the moment, I am investigating where the differences come from. A full investigation should add the tropical storms and winter storms as well.

As a covariate I use low-pass filtered global mean temperature. Let's compare the current climate, 2014, with 1951. There are two options to include the observed extreme. The first is to wait until the data is available in the GHCN-D database. This is updated daily at NCDC, but only monthly in the Climate Explorer. Either wait until the next month or ask me to run the update by hand. The second option is to specify the value reported from another source in the form (after converting from inches to mm for the US). Finally, we scale the distribution with the global mean temperature, which is often a good choice for precipitation . (I am working on the option to fit location and scale parameters independently.) This should give output similar to the following.

JJA gdcnprcpall max_PRCP [mm/day] dependent on GISS global temperature
covariatie 1951 = -0.85208E-01
covariatie 2014 = 0.60375
parameteryearvalue95% CI
N:  1985 
Fitted to GEV distribution P(x) = exp(-(1+ξ(x-a')/b')^(-1/ξ))
with a' = a exp(αT/a) and b' = b exp(αT/a)
a': 1951 59.735 58.881... 61.108
b': 1951 18.088 17.670... 19.299
a': 2014 69.271 68.422... 70.636
b': 2014 20.976 20.533... 22.308
ξ: 0.108 0.087... 0.164
α: 13.323 9.766... 19.214
return period 2014 1951 9632.6 2298.9 ... 17188.
(value 343.20 ) 2014 3456.1 929.36 ... 5142.9
 ratio 2.7871 1.9337 ... 4.1662
This shows that a significant trend α has been detected in the fit. The return time of the 2014 event is now around 3500 years per stations (or 70 years in one of these 50 stations), with a very wide 95% confidence interval of 900 to 5000 years. However, around 1950 it would have been much longer about 10000 years (2000 to 17000). The frequency has increased by a factor two to four, so no change (a ratio of one) is excluded at 95% confidence.

Graphically, this is shown in the following plot. Note that the observations are drawn twice, once downscaled to the 1951 climate and once upscaled to the 2014 climate using the fitted trend. The fact that the GEV distribution is a good fit to the observations show that we do not have problems with double populations that would impair the ability to extrapolate the soft extremes to study this hard extreme.

JJA stations gdcnprcpall with the effects of GISS global temperature scaling the position and scale parameters parameter a,b, referenced at 1951 and 2014
Decreasing return times of precipitation extremes (1951 vs. 2014)

The ratio of return times is often a number that is communicated, so a separate plot is drawn at the end of the page showing the CDF of this ratio derived from a non-parametric bootstrap procedure. TODO: convert this to a FAR distribution. In this case a ratio of one is excluded.

CDF of the ratio of the return times of 2014 JJA stations gdcnprcpall in the climates of 2014 and of 1951
CDF of the difference in return times of 2014 and 1951

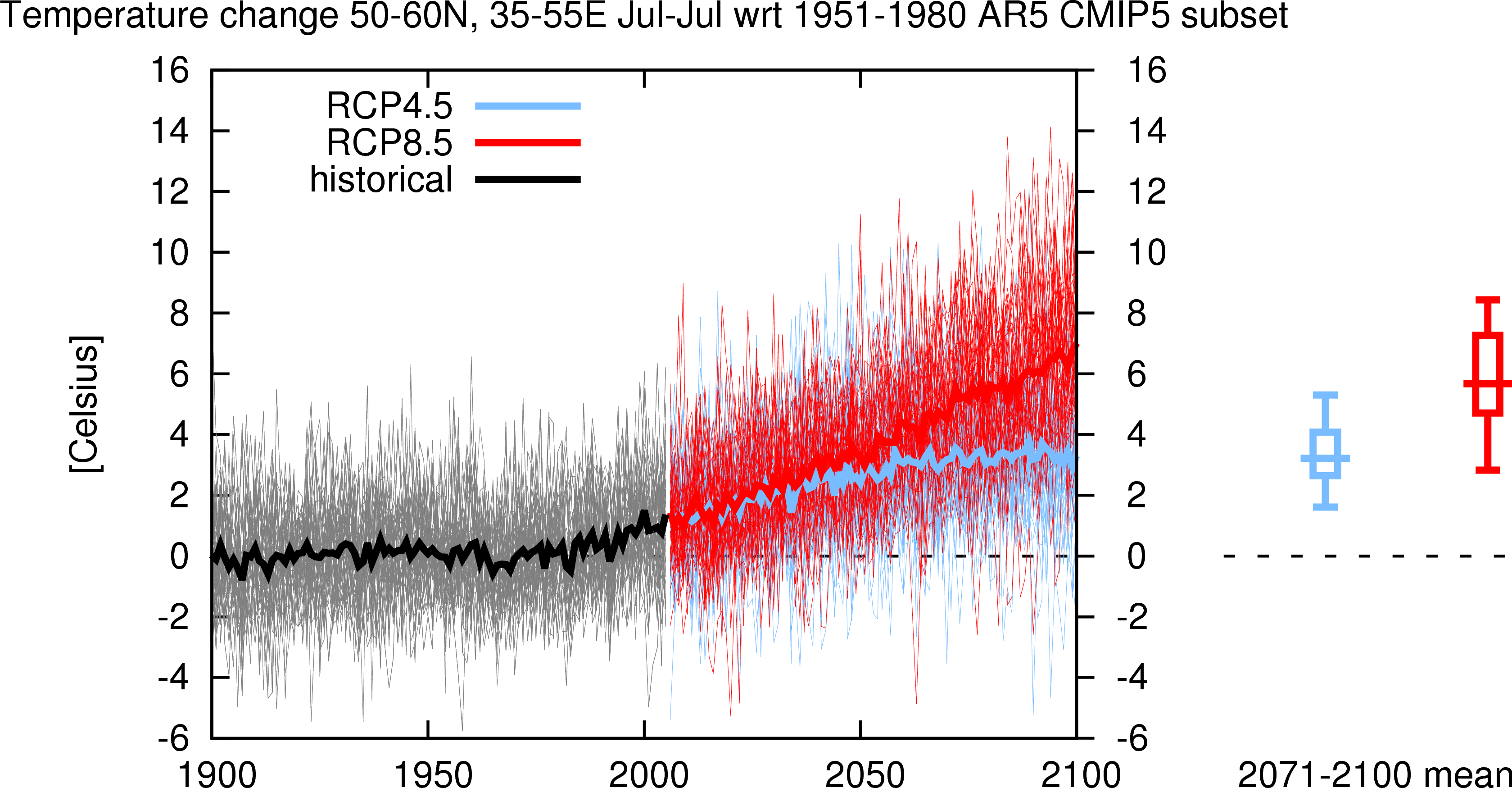
Now that a trend has been detected in the observations, we turn to the theory. Increases in daily precipitation extremes have been found in the data and in climate model output, and are expected on the basis of physics. Temperatures in this part of the world have risen and this rise has been attributed to anthropogenic influences. When I finished writing the paper I will add the quantitative numbers here that conclude the attribution study.